Temper-3D

Для проведения корректных теплотехнических расчетов необходимо придерживаться следующих правил:

1. Определить область охвата (цель, которую вы преследуете). Это может быть достаточно серьезный проект, связанный с разработкой нового узла на стадии проектирования, который требует очень корректного подхода с подготовкой соответствующей документации. Также это может быть расчет, связанный с проверкой (подтверждением) уже существующей конструкции, для того чтобы убедиться в корректности соответствия требованиям СНиП, а также для проведения мероприятий с возможностью выдачи рекомендации по нахождению рационального конструкторского решения. В данном случае достоверность полученных результатом не должна вызывать никаких сомнений. Иногда теплотехнический расчет производится с целью оценки, когда не требуется высокая точность и не требуется документального подтверждения.
2. Определиться с ресурсами, которые требуются для достижения требуемого результата. Это, прежде всего программное обеспечение (ПО), в настоящее время очень популярным является метод конечных элементов (МКЭ) и наличие экспериментального оборудования (тепловизоры, термометрирование в камерах и др.). Хорошо, если численный эксперимент подтверждается результатами эксперимента, но следует иметь в виду, что численный эксперимент намного дешевле натурного, кроме того, численный эксперимент позволяет на стадии проектирования произвести серию теплотехнических расчетов и найти рациональное конструкторское решение. При выборе ПО, предпочтение надо отдавать программам, имеющим отечественные сертификаты соответствия. Вопрос о использовании ОС, а также наличии современного графического интерфейса, важного значения не играет, главное, чтобы ПО могло производить теплотехнические расчеты, с высокой точностью сложных объектов. ПО должно гарантировать корректность полученных результатов. Имеет смысл произвести сопоставление расчета с расчетом имеющим аналитическое решение, в этом случае допустимая погрешность не должна превышать 0,01 °С и даже меньше.
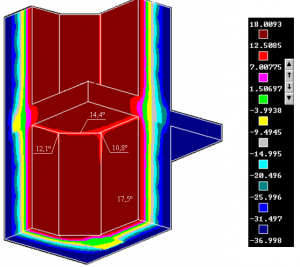
3. Определиться с выбором модели для проведения теплотехнического расчета (одномерная, двухмерная либо трехмерная), также является ли расчет стационарным, либо это нестационарный и, к тому же, нелинейный расчет. Если вопрос о нестационарности и нелинейности практически нигде не рассматривался, что вполне оправданно, то выбор модели, будь то одномерный, двухмерный или трехмерный расчет, является очень важным. Например, одномерный расчет, можно вполне выполнить на калькуляторе и при этом точность при такого расчета будет абсолютно той же, как если бы мы использовали программу для расчета одномерного теплотехнического расчета, при этом следует иметь ввиду, что стоимость проведения такого расчета ничтожна, как впрочем, и достоверность полученных результатов (такой расчет, как правило не имеет ни чего общего с реальным расчетом, погрешность может достигать 100% и более), данный расчет можно использовать только для оценки порядка теплопотерь. Многие задачи можно рассчитывать как двухмерные, на практике в большинстве случаев так и поступают, к тому же, если учесть, что большинство программ для расчета температурных полей могут проводить теплотехнические расчеты только в двухмерной постановке. Однако реальные объекты ограждающих конструкций (ОК) являются трехмерными и представление их в виде плоских фигур  в большинстве случаев совершенно не оправданно. На рис. 1 приведено температурное поле фрагмента ОК, как видно из рисунка фрагмент является трехмерной фигурой, а представление его в виде плоской фигуры, означает, что учет плит перекрытия невозможен, а, как видно из рисунка, именно в данной области образуется зона с температурой 10,8 °С, что значительно ниже точки росы (будет выпадать конденсат), т.е. при использовании программ производящих теплотехнические расчеты в плоской концепции не представляется возможным выявить мостики холода характерные для реальных трехмерных объектов. При решении задачи представленной на рис. 1 в плоской постановке было бы получено вполне приемлемое решение, где не наблюдалось бы зон с температурой ниже точки росы, а это совершенно неверно.
   

   Рис 1. Пример теплотехнического расчета трехмерного узла

   Поэтому для получения реальной картины распределения температур необходимо использовать программы производящие теплотехнические расчеты в трехмерной постановке, либо проводить натурный эксперимент.

4. Определиться с точностью проведения теплотехнического расчета. В научной литературе встречается информация о том, что расчет требуется производить с абсолютной точностью 0.1 С, что соответствует 0.5% относительной точности, при температуре 20 С, это очень высокая точность. Ни один из параметров входящих в расчет (температура, линейные размеры ОК, коэффициенты теплопроводности и др.) не задаются с такой точностью. Тем не менее, если принято решение о том, что расчет следует проводить с точностью, например 0.1 o С, то необходимо проанализировать, может ли выбранное ПО, обеспечить данную точность, при расчете конкретного узла. Если расчетная область достаточно большая и сложная, а требуется провести расчет в трехмерной постановке с высокой точностью, то может оказаться, что количество КЭ окажется слишком большим (больше предельно-допустимых значений для данного ПО). В программе «TEMPER-3D» максимально-допустимое значение количества узлов составляет 5 млн., чем мельче КЭ сеть тем точнее результат. Если же выбранное ПО позволяет производить теплотехнические расчеты, например, только в 20-40 тыс. узлов, то получить высокую точность расчета при достаточно крупной расчетной области будет затруднительно, или даже невозможно. Возникает вопрос о том, как определить погрешность с которой произведен расчет, если нет точного (аналитического) решения? В научной литературе принято считать, что решение с использованием МКЭ найдено с заданной точностью, если оно монотонно (асимптотически) сходится при измельчении КЭ сети в несколько раз. Иными словами, чтобы оценить точность расчета, необходимо провести серию расчетов, например 4-6, при этом на каждом этапе сгущая КЭ сеть в два раза. После этого анализируются полученные теплотехнические расчеты, если решение монотонно сходится, то находиться асимптота, к которой сходится это решение. Данное решение (асимптота) считается «точным» решением, затем вычисляется абсолютная погрешность, как разница между «точным» решением и текущим для каждой точки КЭ сети. Наибольшая по модулю разность по всем точкам КЭ сети, принято считать погрешностью. При использовании программ, где КЭ сеть генерируется автоматически, это возможно только в двухмерных расчетах, пользователь может и не знать какого размера КЭ и их количество. Погрешность, с которой произведен расчет так же, как правило, неизвестна. Поэтому необходимо, на сколько это возможно, произвести несколько расчетов, при различной степени дискретизации, и сравнить результаты, расхождение не должно превышать заявленной абсолютной точности расчета. При расчете плоских областей, как правило, не возникает проблемы с нехваткой КЭ (10-50 тыс узлов КЭ сети вполне достаточно), при этом КЭ имеют достаточно небольшие размеры, и тем самым гарантируется высокая точность расчета. При расчете сложных трехмерных объектов, для получения приемлемой точности, требуется гораздо большее количество КЭ, чтобы обеспечить достаточно мелкое разбиение. Как, правило, для реальных расчетов с приемлемой точностью, не очень больших объектов требуется от 20 до 200 тыс. узлов КЭ сети. Максимальное количество узлов КЭ сети в программе «Temper-3D» достигает 8 млн. Для проведения таких расчетов требуются высокопроизводительные ПК, с частотой микропроцессора 2Ггц, и объемом оперативной памяти не менее 2 Гб, так же требуется наличие высокопроизводительного видеоадаптера. Время расчета в значительной степени зависит от вида расчетной области, задания граничных условий, типов используемых материалов и колеблется от нескольких десятков секунд, до нескольких минут. В программе «Temper-3D», после проведения расчета на экране монитора показываются области, в которых погрешность расчета, превышает заданную. В этом случае, если погрешность велика, то требуется дополнительно измельчить КЭ сеть, делается это автоматически, после измельчения КЭ сети задавать граничные условия и характеристики материалом не требуется, необходимо, только еще раз выполнить расчет.
5. Определиться с выбором расчетной области. Это очень важный момент, необходимо произвести «идеализацию» расчетной области, т.е. отбросить не существенные или малозначимые элементы. Стараться по возможности, чтобы расчетная область была, как можно меньших размеров, тогда можно будет более детально разбить область на КЭ, кроме того, чем меньше область, тем более мелкую КЭ сеть можно использовать и тем самым повысить точность расчетов. В качестве расчетной области надо выбирать симметричную часть, причем симметрия должна быть, не только с геометрической точки зрения, но и с точки задания граничных условий. Т.е. отсечение расчетной области должно происходить по осям симметрии , вновь полученные грани в дальнейшем будут теплоизолированы (в пункте Граничные условия надо задать коэффициент теплоотдачи равным 0). От способа идеализации в значительной степени зависит корректность всего расчета, излишнее упрощение может привести к неправдоподобным результатом, а излишняя детализация может значительно усложнить подготовку данных для расчета, и при этом не позволит существенно увеличить точность всего расчета. На рис.2 (схематично показан фасад с оконными проемами) приведен пример неправильного (а и b), и правильного (с) выбора расчетной области.
   

   Рис 2. Правильный и неправильный выбор расчетной области

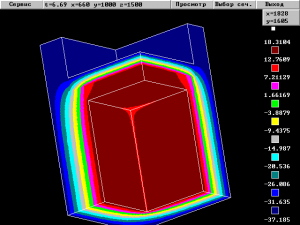
   В варианте (b), на верхней грани расчетной области, может возникнуть тепловой поток, в связи с отсутствием симметрии. Если бы оконный проем сверху был прямоугольным, а не закругленным, то данный вариант был бы самым предпочтительным, так как имеет наименьшие размеры, однако это возможно только в случае, когда плита перекрытия расположена посередине между оконными проемами, т.е. расстояние от пола до нижней части окна равно расстоянию от верхней части окна до потолка, что на практике, как правило, не наблюдается. В варианте (с), по верхней и нижней граням также нет полной симметрии, но асимметричные участки достаточно удалены от грани расчетной области. Кроме, того, в варианте (с) дополнительно имеется возможность после проведения расчета, убедиться в конгруэнтности (равенстве) температурных полей верхней и нижней граней (должно быть хорошее совпадение). Поэтому, несмотря на то, что вариант (с), имеет больший размер, чем вариант (b), тем не менее, он более предпочтителен, так, как большая асимметричность может внести существенную погрешность в расчет. Сложнее обстоит вопрос с выбором расчетной области и ее идеализации при использовании программ с двухмерным распределением температурного поля. Практически любая реальная конструкция, не может быть представлена в виде плоской фигуры, поэтому уже при выборе расчетной области, уже изначально закладывается погрешность в будущий расчет, причем эта погрешность может достигать 30-40%, что совершенно не допустимо. Поэтому для выполнения реального проекта, необходимо производить расчеты в плоской постановке, только для очень простых областей. Сложные области (углы, балки, гибкие и жесткие связи и другие неоднородности) не могут быть учтены в двухмерной постановке. Для таких объектов необходимо, либо использовать трехмерные идеологии, либо проводить натурный эксперимент. Для снижения погрешности, или по крайней мере для ее оценки, необходимо производить идеализацию различными способами, а затем сравнивать значения температурных полей в одних и тех же точках, если отличие будет превышать 1 °С, то достоверность расчетов будет вызывать сомнение, несмотря, на то, что программа по расчету будет производить вычисления с высокой точностью. На рис. 3 приведена угловая конструкция рассчитанная с помощью программы «Temper-3D», из рисунка видно, что температурное поле имеет существенно трехмерный характер распределения, наиболее низкая температура внутренней поверхности наблюдается в углу, что вполне разумно и составляет 6.69 °С в точке x=660; y=1000; z=1500, что гораздо ниже точки росы и является неприемлемым.

   

   Рис 3. Температурное поле трехмерного объекта, температура в углу равна 6,69 °С

   

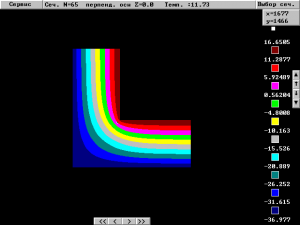
   Рис 4. Двумерное температурное поле рассчитанное по оси перпендикулярной оси Z, температура в углу равна 11,73 °С

   

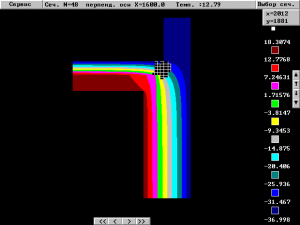
   Рис 5. Двумерное температурное поле, рассчитанное в сечении перпендикулярной оси X (при X=1600мм) (черными элементами показан фрагмент, где погрешность превышает допустимую 0,1 °С). Температура в углу равна 12,79 °С

   

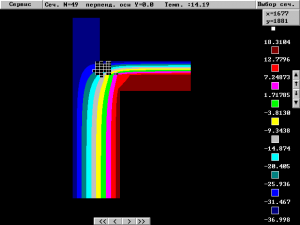
   Рис 6. Двумерное температурное поле, рассчитанное по оси перпендикулярной оси Y (черными элементами показан фрагмент, где погрешность превышает допустимую) температура в углу равна 14,19 °С

   Если данную конструкцию рассчитать с помощью плоского алгоритма, то в зависимости от способа выбора сечения получаем температурные поля на рис. 4 , рис 5. и рис 6. соответственно. Как видно из рисунков температура в углу составляет 11,73 °С, 12,79 °С и 14,19 °С, для различных способов идеализации, что выше точки росы. По результатам плоского расчета, видно, что выпадение конденсата в углу не наблюдается, в то время, как объемный расчет показывает, в углу будет обильное выпадение конденсата. Относительная погрешность вычисления температуры в углу, в лучшем случае составляет W=|(6,69-11,73)|/6,69*100=75,3%, в худшем 112%, а абсолютная погрешность составляет от 5 °С до 7,5 °С, что совершенно не поддается объяснению. Иными словами, использование плоской (двумерной) концепции, уже на стадии выбора расчетной области подразумевает, что погрешность будет очень велика, поэтому требовать от плоской модели точности 0,1 °С представляется не обоснованным.

6. Определить степень дискретизации, и определить погрешность, от данного способа дискретизации (это в следующей статье).

Выводы:

При возникновении вопроса, о том, как произвести корректный теплотехнический расчет, следует следовать следующим рекомендациям:

• Если проект серьезный, то использование двумерных технологий не годится в принципе (погрешность будет составлять 30%-100%). Возможна альтернатива в виде натурного эксперимента (это достаточно дорого). Использовать только сертифицированные на отечественном рынке программы.
• При использовании ПО необходимо убедиться, что точность полученных результатов не вызывает сомнения (результаты произведены с требуемой точностью). Утверждение, о том, что программа считает с точностью до 0,1 °С, и при этом расчет производится в плоской либо линейной постановке не обоснован.
• При использовании программ с трехмерной концепцией, следует убедиться, что возможен расчет с достаточно большим числом узлов, который даст возможность произвести корректные расчеты.
  Время расчета, графический интерфейс, сложность подготовки исходных данных, ОС, цена и др. является второстепенным.
• Особое внимание следует уделять технической поддержке проекта.

ЛИТЕРАТУРА

1. СНиП II-3-79**. Строительная теплотехника / Госстрой СССР. -М.,1986. — 32с.
2. Руководство по теплотехническому расчету и проектированию ограждающих конструкций зданий/ НИИСФ. -М.:Стройиздат, 1984. — 141 с.
3. Расчеты и проектирование ограждающих конструкций зданий: Справочное пособие к СНиП / НИИСФ. -М.:Стройиздат, 1990. — 233 с.
4. О принятии изменения №3 строительных норм и правил СНиП II-3-79**”Строительная теплотехника”: Постановление Министерства Строительства Российской Федерации № 18-81 от 11.08.95 г.
5. СНиП 2.01.01-98. Строительная климатология и геофизика / Госстрой
   СССР. -М., 1983. — 136с.
6. СНиП 2.08.01-89. Жилые здания / Госстрой СССР. — М., 1990. -16с.
7. Руководство пользователя программой ”TEMPER” по расчету температурных полей ограждающих конструкций. (Учебно-методическая разработка). Омск, СибАДИ, 1997. – 36с.
8. Методическое пособие по теплотехническому расчету ограждающих конструкций зданий. Омск, СибАДИ, 1996. – 43с.
9. СНиП 23-02-2003 Тепловая защита зданий / Госстрой СССР.-М.,2004. – 27 с.
10. СП 23-101-2004. Проектирование тепловой защиты зданий /Госстрой СССР. -М., 2004. – 141 с.
11. Свидетельство об официальной регистрации программы для ЭВМ «TEMPER-3D» №2006610359 от 20.01.2006 г. (правообладатель Федоров С.В.)