Федоров С.В. канд. тех. наук. г. Омск
В последнее время при расчете температурных полей ограждающих конструкций (ОК) очень популярен метод конечных элементов (МКЭ). Имеется значительное количество программных комплексов (отечественных и зарубежных), позволяющих решать данную задачу, как в плоской, так и в трехмерной постановке. При реализации МКЭ, используются различные конечные элементы. В плоской модели, это, как правило, треугольные и четырехугольные, а в объемной постановке – тетраэдры и параллелепипеды, причем не обязательно прямоугольные (изопараметрические), см. табл. 1. Иногда используются КЭ более высокого порядка (кубические), кроме того, могут быть использованы специальные, так называемые сингулярные элементы, которые используются, например, в механике разрушения. В данной таблице так же не приведены одномерные элементы, стержневые и др.
Пользователь вправе выбрать, использование различных типов элементов, конечно с учетом, того, хочет он решать плоскую или объемную задачу. Однако от закона распределения функции формы, особых преимуществ получить не удастся *.
* Прим. автора.
При проведении численного эксперимента, оказалось, что использование различных элементов, не выявлено превосходства какого-либо типа элемента. Например, использование большего количества линейных элементов, не ведет к увеличению времени расчета, для достижения наперед заданной точности по сравнению к квадратичным. Что касается треугольного или четырехугольного элементов, то следует, при сложной форме использовать треугольники (тетраэдры), а для простых тел четырехугольники (параллелепипеды).
Доказано [3], что при измельчении КЭ сети решение монотонно сходится к точному (чем мельче бьешь, тем выше точность). Однако, где предел измельчению? И, кроме того, как узнать, что проведенный расчет, при данной степени дискретизации, можно считать приемлемым. Т.е. необходимо дать оценку, на стадии дискретизации.
В данной работе приведен анализ, степени дискретизации КЭ на точность расчета. В качестве примера использован трехмерный восьмиузловой КЭ, однако данный анализ можно распространить и на другие типы элементов.
Известно, что, для получения «точного» решения, иногда требуется всего несколько КЭ (для расчета трехслойной ОК достаточно всего 3 элементов), а для проведения расчета однородной конструкции типа «угол», требуется несколько тысяч КЭ.
Пользователь иногда (а, как правило, всегда), мельчит КЭ сеть там, где это совсем не требуется и, наоборот, использует грубое разбиение там, где надо измельчать КЭ сеть. При этом результаты расчетов могут быть искажены на 30-1000% и более, что не допустимо.
При расчете МКЭ, вводиться несколько понятий точности, а именно:
- Точность при выборе (идеализации) расчетной области.
- Точность при решении системы линейных уравнений.
- Точность расчета баланса входящих и выходящих потоков.
- Точность полученных результатов для данной расчетной схемы.
Что касается корректности выбора расчетной области, это отдельный, очень важный вопрос, который не рассматривается в данной работе.
Точность решения СЛАУ, как правило, не особо влияет, на конечную точность, но следует иметь в виду, что если завышать точность, то значительно увеличится время расчета (при итерационных методах решения СЛАУ). Рекомендуется использовать точность для данного параметра 1,0 Е-05 — 1,0 Е-06 от габаритного размера расчетной области [1].
При оценке точности входящих и выходящих потоков допустимо значение до 1% [2], в программе «Temper-3d» [2], допустимая точность 0,01%, после этого выдается предупреждение. Но оно может быть вами игнорировано (если погрешность более 1%, то корректность расчета вызывает сомнение). Следует учесть, что неоправданное измельчение КЭ сети ведет к увеличению погрешности по данному параметру. См. табл. 2 и рис. 16, однако, все равно желательно, чтобы погрешность не превышала 0,1%.
Что касается точности полученных результатов, то в литературе данный вопрос не рассмотрен, кроме того, даже не дан параметр, по которому следует оценивать данную погрешность. Оценивать погрешность в % (относительная погрешность) не является корректным, потому что, если например «точное решение» 0,01 С, а в результате расчета вы получили 0,03 С, то погрешность будет 300%, в то время как абсолютная погрешность всего 0,02 С.
Поэтому, в данной работе будет рассматриваться не относительная, а абсолютная погрешность, что вполне разумно. Допустимые диапазоны изменения данного параметра 0,1 С – 0,2 С. Требовать большую точность не вполне оправданно, так как остальные параметры (размеры, температура внутреннего воздуха, коэффициент теплопроводности, и др.) не могут быть заданы с достаточной точностью. Реально погрешность даже в 0,2 С вполне приемлема.
Для оценки степени дискретизации на точность расчета расчетной области (не следует путать с реальной точностью, так как реальная точность зависит от множества других параметров, таких как корректный выбор расчетной области, выбор типа элемента и др.) проведен численный эксперимент.
В данной работе расчеты проводились с помощью программы «Temper-3d». В качестве конечного элемента используется трехмерный, восьмиузловой конечный элемент.
Расчеты (для упрощения) проводились в плоской постановке, но они в дальнейшем были применены к объемной модели без каких-либо изменений, также использовалась однородная конструкция.
Сразу следует отметить, что такой параметр, как размер КЭ, не может служить объективной оценкой (высказывание, на подобие, того, что размер КЭ не должен превышать 20 мм не может быть объективен, потому что, например, при расчете однослойной, или трехслойной ОК достаточно всего одного (трех) КЭ, не зависимо от размера ОК).
Необходимо выбрать критерий (оценку), который бы гарантировал точность расчетов.
Коэффициент теплопроводности был принят lam=0,35, внутренняя температура 20С, наружная -37, коэффициенты теплоотдачи 8,7 и 23 соответственно.
В качестве исследуемых параметров были выбраны – температура внутреннего угла, и Ro.
Расчеты проводились при различной степени дискретизации, была использована равномерная сетка (строки 1-8), а также неравномерная КЭ сеть (строка 9).
Как видно из табл. 2 и рис. 14, решение монотонно сходится, даже при более, чем 4 млн. узлов, что свидетельствует о корректности проведенных расчетов.
Где:
1- N*N -количество элементов в области 640*640 мм.
2- Nz- количество узлов КЭ сети
3- L-размер КЭ в мм
4- Tmin-температура внутреннего угла
5- Ro конструкции, рассчитанного по наружной поверхности ОК
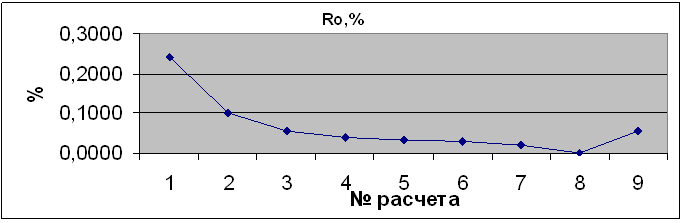
6- Погрешность при расчете Ro, % (в качестве точного решения принят расчет №8)
7- Погрешность входящих и выходящих потоков, %
8- DT- Максимальное искажение температур в КЭ (Tmax=(T1+T3)-(T2+T4)), С. Т.е. насколько отличается (искажена) среднее арифметическое диагонально расположенных узлов, от другой пары, диагонально расположенных узлов (четырехузловой элемент, в случае объемного КЭ, рассматривается каждая грань)
9- Tmax- Абсолютная погрешность, С
Анализируя результаты расчетов можно сделать вывод, что для получения требуемой точности расчета (<1%, при этом точность в вычисление температуры составляет менее 0,1 С, что вполне допустимо), необходимо производить дискретизацию с равномерным шагом не более 32 мм, при этом погрешность вычисления Ro<0.05%, для этого надо использовать 4242 КЭ, при использовании неравномерной КЭ сети, для получения не меньшей точности, требуется всего 858 узлов КЭ сети.
При большей точности выигрыш получается еще большим. Причем следует обратить внимание на то, на сколько неравномерна КЭ сеть (отношение максимального элемента к минимальному около 40).
При расчете в «TEMPER-3D», необходимо установить максимальное искажение температур в КЭ, после этого на экране КЭ в которых перепад будет большим будут выделены черным цветом. На рис. 17 Приведено температурное поля с изображением КЭ у которых искажение более 0.1 С, расчет №3. На рис. 18 изображено температурное поле и обозначены КЭ в которых искажение температур более 0,2 С.
Выводы:
- При расчете температурного поля ОК, следует особое внимание уделять, не только степенью приближения идеализированной конструкции к реальному объекту (что очень важно), но и способу рациональной дискретизации конструкции на КЭ, причем отношение размера к минимальному размеру КЭ, может быть 20-100 и более, при этом происходит существенная экономия КЭ даже в плоской модели, не говоря уже о трехмерной. «Сэкономленные» КЭ, в дальнейшем можно использовать для более детальной дискретизации. Экономия может составлять несколько тысяч %. Утверждение, что точность определяется величиной КЭ не корректно.
- Для подтверждения корректности проведенных расчетов необходимо убедиться, что максимальное искажение температур в любом элементе не превышает наперед заданной величины (1-0,1С), при этом абсолютная погрешность не будет превышать 0,1С при Tmax<0,5С. Данная методика успешно используется уже в течение многих лет, при расчетах трехмерных ОК.
Литература:
- О выборе шага по времени при решении нестационарных задач теплопроводности методом конечных элементов. (Статья). Деп. в ВИНИТИ N 8493, В 87, 1988.
- Программный комплекс для расчета двухмерных температурных полей в ограждающих конструкциях зданий. Министерство науки и техн. Политики РФ \Ротапринт Омского ЦНТИ,Росинформресурс Омск,1995.4с.
- О Зенкевич. Метод конечных элементов
- Оден Нелинейная механика сплошных сред
- Свидетельство об официальной регистрации программы для ЭВМ «TEMPER-3D» №2006610359 от 20.01.2006 г. (правообладатель Федоров С.В.)